What is the Archimedean spiral in a gear hob?

An important element of the gear hob design is the tip which represents a relief of the tooth profile and a part of the Archimedean spiral.
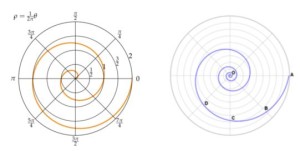
The Archimedean spiral is a curve traced out by a point moving in such a way that its movement towards or away from the center is uniform with the increase of its vectorially angle from the starting line. This curve is used to ensure the continuity of the tooth profile during the resharpening.
For a resharpening with a zero-rake angle, the cutting profile lies on a plane that passes through the hob axis and the Archimedean spiral must ensure that the profiles that are on this perpendicular section are constant. This curve is used in the tooth profiles of the gear hob.
The characteristics of the Archimedean spiral are:
- In Archimedes spiral, any ray passing through the origin does intersect successive turns of the spiral with a constant distance which is equal to 2 π Therefore, it is also named “arithmetic spiral”.
- An Archimedes spiral, there are two arms – one arm for θ> 0 and another for θ < 0. These two arms are connected to the origin. One arm is shown in the graph. If we take the mirror image of this arm along Y axis, the other arm will be obtained.
- Usually the term Archimedean spiral is used for more general spirals. The normal one occurs when in its equation, n = 1. Other spirals that fall into this group are the Fermat’s spiral and the hyperbolic spiral.
- All the static spirals are logarithmic spirals in nature, except for Archimedes spiral.